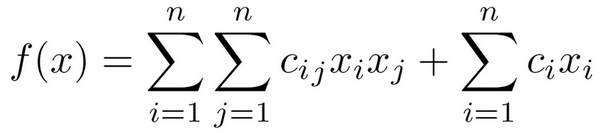Members: Sitapa Rujikietgumjorn and Robert T. Collins

Optimized Pedestrian Detection for Multiple and Occluded People

S.Rujikietgumjorn and R.Collins, "Optimized Pedestrian Detection for Multiple and Occluded People" IEEE Computer Vision and Pattern Recognition (CVPR'13), Portland, OR, June 2013, pp.3690-3697.

Abstract

We present a quadratic unconstrained binary optimization (QUBO) framework for reasoning about multiple object detections with spatial overlaps. The method maximizes an objective function composed of unary detection confidence scores and pairwise overlap constraints to determine which overlapping detections should be suppressed, and which should be kept. The framework is flexible enough to handle the problem of detecting objects as a shape covering of a foreground mask, and to handle the problem of filtering confidence weighted detections produced by a traditional sliding window object detector. In our experiments, we show that our method outperforms two existing state-of-the-art pedestrian detectors.

Framework

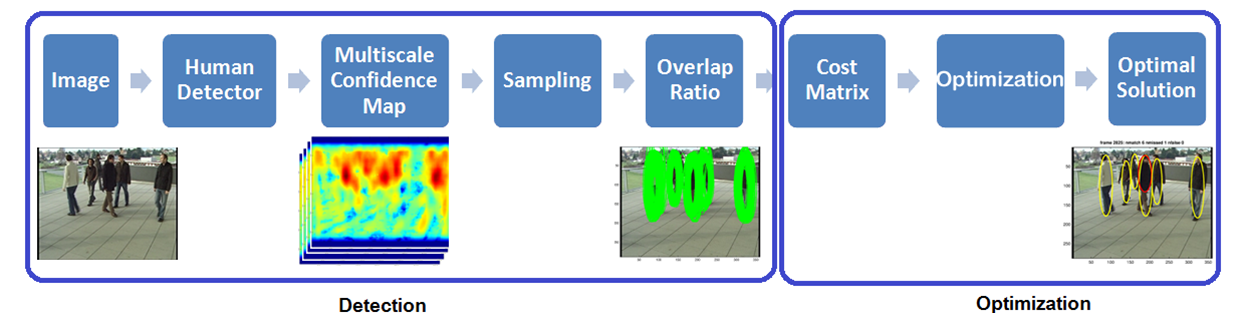An overview of our proposed method

Generating a Set of Detection Candidates

We show two approaches for generating a set of detection candidates.

Detection Candidates by Shape Covering: Unary confidence scores are computing using
Detection Candidates by Bounding Box Filtering: Histogram of Oriented Gradients (HOG) based pedestrian detector without non maximum suppression

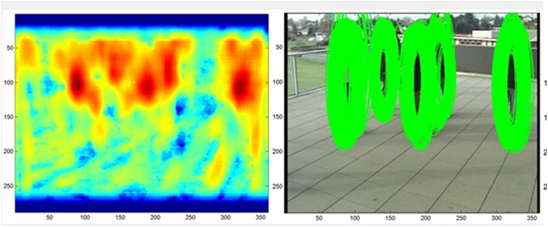
Optimization

We select the best set of candidates using Quadratic Unconstrained Binary Optimization (QUBO) framework. Our quadratic objective function is

where x is binary variables, ci are unary coefficients, and cij are pairwise coefficients. The goal is to assign 0,1 values to each xi in a way that maximizes the objective f(x). We can combine all the coefficients ci and cij into a single square matrix Q and solve the binary integer maximization.

The resulting Quadratic Unconstrained Binary Optimization (QUBO) problem is known to be NP-hard.

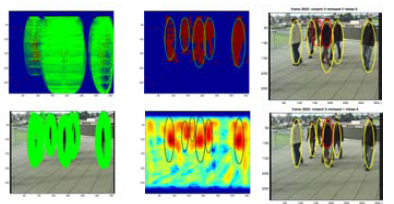
The following figure is a simple example showing a solution from QUBO framework

 

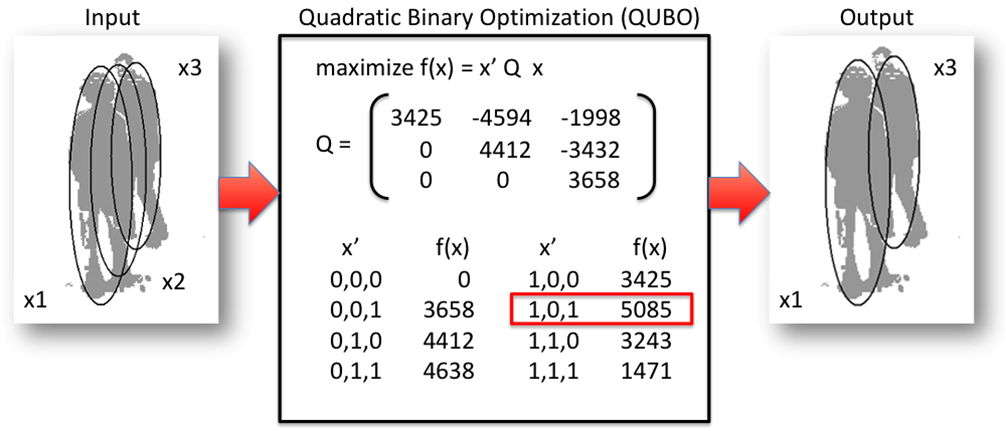Experimental Results

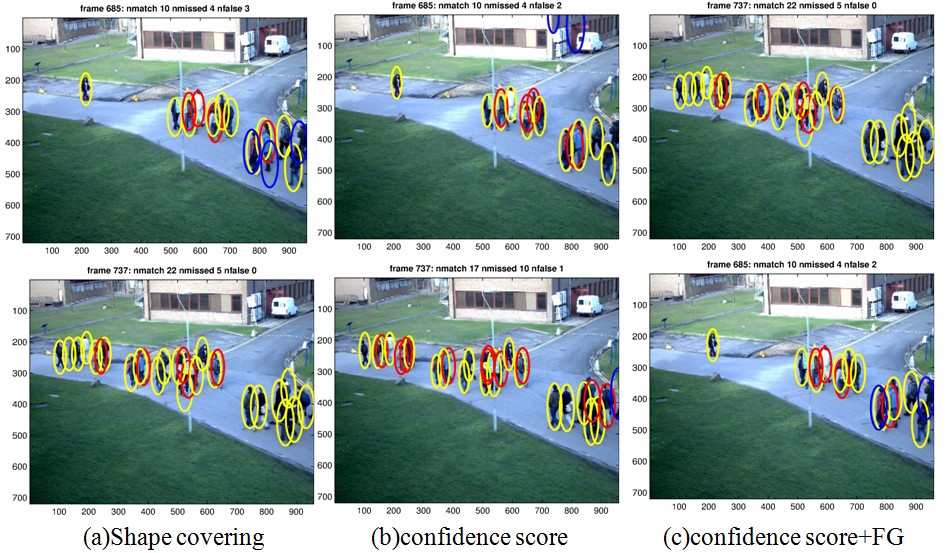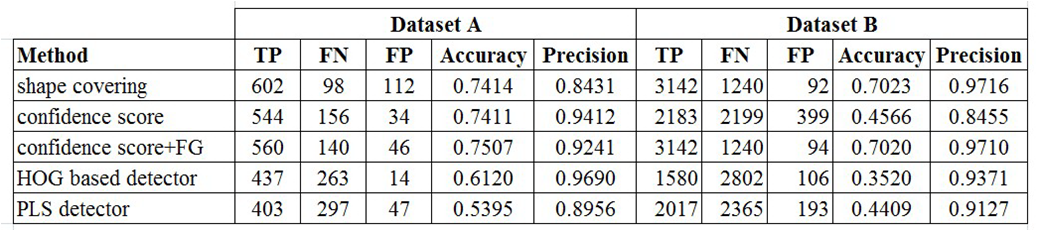Conclusion

We have presented a QUBO framework for improving pedestrian detection performance in cases where there are multiple, overlapping objects. A quadratic objective function is formed from unary confidence scores and pairwise overlap penalties. The unary terms are not limited to a specific type of detector and can be applied to various types of detection confidence scores. Solving for the binary solution vector that maximizes this quadratic objective function automatically balances the trade off between encouraging multiple, high quality detections, while discouraging excessive amounts of overlap.

Acknowledgement

This work was partially funded by NSF grant IIS-1218729