Introduction

A regular wallpaper pattern can be generated by two basis vectors, (t1, t2). The lattice generated by (t1, t2) divides a 2D plane into identical parallelograms, called tiles. Given the natural match between tiles/basis-vectors in wallpaper theory, and observable nodes/edges in probabilistic graph models, we can encode domain knowledge from wallpaper theory into the observation model and pairwise compatibility function of a degree-4 Markov Random Field (MRF). Belief Propagation (BP) can then be used to locate a deformed lattice in an unsegmented image.

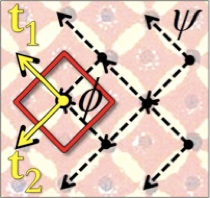
Motivation

An automatic, robust and fast lattice detection algorithm can facilitate novel applications in 1) automated near-regular texture (NRTs) analysis and manipulation 2) photo editing for Image Defencing, 3) Geo-tagging, 4) 3D modeling, and 5) video replacement.

(1) Liu et al "NRT analysis and manipulation" SIGGRAPH2004

(2) Liu et al , "Image de-fencing", CVPR2008

            (3) Shindler et al, “Geo-tagging”, CVPR 2008                                 (4) Google Earth 

5. (5)W.C. Lin and Y. Liu, “, A Lattice-based MRF Model for Dynamic Near-regular Texture Tracking”, PAMI 2007 - Semi-automatic  initialization of lattice before tracking and low lattice detection rate (22%)
   

Overview of Algorithm

There are three phases: lattice model proposal, spatial tracking, and incremental thin-plate spline warping.

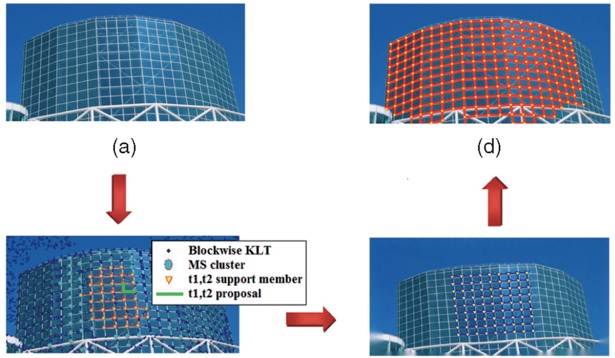
Intermediate results illustrating stages of the lattice finding algorithm. (a) Input image. (b) Lattice model proposal (result of Phase I). (c) Intermediate result after one iteration of MSBP and TPS warping (Phases II and III). (d) The final detected lattice.

Phase I

Phase I results: The green L-shape inside the red enlarged rectangular window is the proposed (t1; t2) vector pair, and the red L-shapes are its supporting members (inlier votes). The images are cropped to emphasize the area of interest.

Phase II & III

We treat the discovery of the deformed lattice in an image as a multi-target tracking problem. Once a partial lattice is found in an image, it is natural and useful to relate the found lattice to its regular origin since straightening out (rectifying) the deformed lattice and its neighborhood helps the iterative algorithm to expand its search for larger and larger lattice structures in the image.

Experimental Results

We compare lattice detection results of our approach against two state-of-the-art algorithms, the method of Lin and Liu [13], [14], and the method of Hays et al. [12]. Since the work of Lin and Liu requires a lattice unit to be given by the user, we do not report its average runtime, and we only report its success rate for the same 32-image data set used in [31]. We extensively compare the automated method of Hays et al. with our proposed method in terms of running time on 261 real-world images and success rate on 143 real-world images. As illustrated in Table below, our detection rate for the 143 images is 65.78 +- 28.79 percent and the rate for Hays et al. is 35.72 +- 39.28 percent. The average running time of our proposed method over that of Hays et al. [12] is close to a 10-fold speed-up on average.

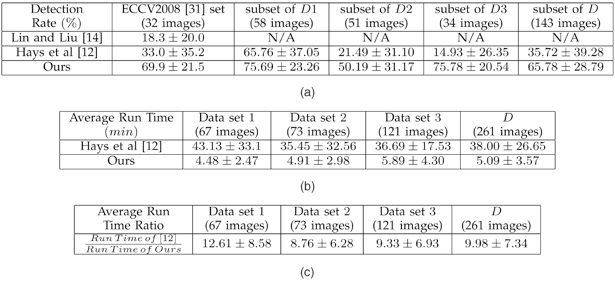
Since we have only ground truth for 143 images available at this time, we report the detection rates for 143 out of the 261 images in the entire data set D. The average running time, however, is for all 261 images in the data sets. The success rate is defined as the ratio of the number of correctly detected texels over the total number of ground truth texels. The runtime ratio is defined by the ratio of the time used by [12] to detect the lattice over the time used by our proposed method. (a) Detection rate. (b) Average running time. (c) Average running time ratio.

Sample Results

Publications

Deformed Lattice Detection in Real-World Images using Mean-Shift Belief Propagation [pdf]

Minwoo Park, Kyle Brocklehurst, Robert T. Collins, and Yanxi Liu.

IEEE Transaction on Pattern Analysis and Machine Intelligence (PAMI). Special Issue on Probabilistic Graphical Models, Volume 31, number 10 in October 2009. Acceptance rate=15%.

Deformed Lattice Detection via Mean-Shift Belief Propagation  [pdf]

Minwoo Park, Robert T. Collins, and Yanxi Liu

European Conference on Computer Vision (ECCV), Marseille, France, October 2008. Acceptance rate=23%

=> Data and MATLAB Code <=

     Please use this linked citation when using the Deformable Lattice

Members: Minwoo Park, Kyle Brocklehurst, Robert T. Collins, and Yanxi Liu.